How do computers represent negative numbers? There are many ways to do this, but nowadays the most popular method is two's complement. This post will build from basic mathematical concepts to a mathematical justification for using this method.
Sets
A few basic ideas from set theory are extremely valuable tools when trying to understand how math is performed on computers.
A set is a mathematical abstraction for a grouping of some items. A common analogy used to describe sets is that a set is like a bag that contains some collection of objects. This is a useful analogy because it captures the essence of what a set is while also illustrating some of the more confusing properties of sets. For example, the empty set, a set which contains nothing, is denoted by the following symbol:
$$\emptyset$$
A set is also often denoted by curly braces; that is, the set begins with the symbol "{" and ends with the symbol "}", and the items in the set are separated by commas. Using this convention, an empty set can also be represented by:
$$\{\}$$
These two symbolic representations are equivalent and interchangeable. Note, however, that the empty set is not equivalent to a set containing the empty set:
$$\{\emptyset\} \not = \emptyset$$ $$\{ \{\} \} \not = \{\}$$
The bag analogy illustrates this nicely. Obviously, an empty bag is not physically the same thing as a bag containing another empty bag. Similarly, a set containing the empty set is not empty.
Not every set is empty. In fact, there are infinitely many different examples of sets that are not empty. To give an example of what one of these would look like, we can consider the set of digits that we use to represent numbers in base 10 (this set is also sometimes called the integers modulo 10):
$$\{0, 1, 2, 3, 4, 5, 6, 7, 8, 9\}$$
So much for sets. Now, we need to introduce a related concept called the relation. A relation is a mathematical construct used to represent certain kinds of relationships between two sets. A relation can represented visually by graphs (often used in algebra) or arrow diagrams (often used in philosophy and logic). A relation between two sets is always a relation from one set to another set.
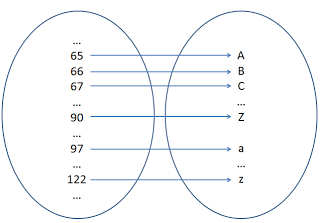
For example, the ASCII table (http://www.asciitable.com/), a tool widely used in programming in the convenient use cases where one does not have to fiddle with Unicode character sets, represents multiple relations in an extremely compact form. One of these relations is a relation between the integers and the letters of the alphabet. This relation can be represented by the following arrow diagram:
For a more thorough explanation of how a function is a certain type of relation, review my prior post, Relations on Pokemon. In this post, we will only discuss properties of relations that are relevant to the theory of two's complement.
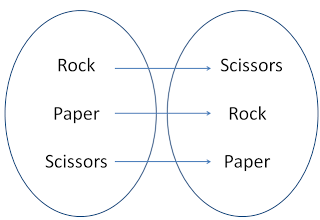
One special way of looking at a relation is to consider it as mapping both to and from the same set. In some cases, this perspective comes more naturally than in others. For example, victory conditions in the classic non-transitive game Rock, Paper, Scissors can be represented by such a relation, where each item is mapped to the choice that it beats:
If you picked a given choice in the left circle above, you would win against the choice in the right circle pointed to by the arrow leading out of your choice. Another way of representing a relation is as a set of ordered pairs, where the first element in each pair is from the domain, and the second element in each pair is from the codomain. The pairs that are present in the relation are exactly those pairs of elements connected by arrows in an arrow diagram. For example, the victory conditions in the game Rock, Paper, Scissors can be represented as the following set:
$$\{ (Rock, Scissors), (Scissors, Paper), (Paper, Rock) \}$$
Every relation has an inverse. The inverse is obtained by swapping the domain and codomain and reversing the order of the arrows, or by simply swapping the elements in each ordered pair. For example, the inverse of the victory conditions for Rock, Paper, Scissors is the set of loss conditions:
$$\{ (Scissors, Rock), (Paper, Scissors), (Rock, Paper) \}$$
Although every relation has an inverse, not every function has an inverse, because we define the inverse of a function to be a functional relation that reverses the relationship in question.
Properties of Relations
Five fundamental properties of relations are listed below:
Reflexivity. A relation R is reflexive on a given set S if and only if, for every element x of the set S, the ordered pair (x,x) is in the relation R. For example, the identity relation contains every pair of the form (x,x); the identity relation on the letters of the alphabet would look like this: {(A,A), (B,B), (C,C), ...}. Clearly, this relation is reflexive.
Irreflexivity. A relation is irreflexive on a set if and only if, for every element x in a set, (x,x) is NOT in the relation. The Rock, Paper, Scissors the Rock, Paper, Scissors victory relation discussed in part 1 is irreflexive because no choice wins against itself; instead, a tie results if both players make the same choice. Curiously, it turns out that it is possible for a relation to be neither reflexive nor irreflexive. This is the case if some elements are related to themselves, and others are not.
Symmetry. A relation is reflexive if and only if, for every pair (x,y) in the relation, its reflection or mirror pair (y,x) is also in the relation. The identity relation described above is symmetric, because if we swap the elements in any given ordered pair in the relation, the mirrored ordered pair is the same, so it is still in the relation.
Antisymmetry. A relation R is antisymmetric on a given set S if and only if, for every pair of elements (x,y) which is both in the relation and also has its mirror pair (y,x) in the relation, x = y (x and y must be the same element). For example, the Rock, Paper, Scissors victory relation discussed in part 1 is antisymmetric. Since Paper beats Rock, Rock does not beat Paper. The identity relation is also antisymmetric, because no two distinct elements are related. (By these definitions, it turns out that a relation can be both symmetric and antisymmetric!)
Transitivity. A relation R is transitive on a set S if and only if for every subset of three (not necessarily distinct) elements {x,y,z} from S, if (x,y) is in R and (y,z) is in R, then (x,z) must also be in R. For example, the less-than sign is transitive; any number that is less than 10 is also less than 100 because 10 is less than 10. Conversely, Rock, Paper, Scissors is often called a "non-transitive game" because although Rock beats Scissors and Scissors beats Paper, Rock does not beat Paper (even though it beats something that beats Paper).
Thanks to Jordan Kodner for correcting me after I confused reflexivity and symmetry in this section.
Equivalence Relations
An equivalence relation is a special type of relation. Any relation which is reflexive, symmetric, and transitive is considered an equivalence relation. For example, the canonical equivalence relation is the identity relation R, where a pair of elements
The identity relation is not, however, the only equivalence relation. In particular, there are two other relations that are of great interest to us when discussing two's complement. The first of these is the relation on the integers indicating equality of absolute value:
$$\{ (0, 0),\ (-1, -1),\ (-1, 1),\ (1, -1),\ (1, 1),\ (-2, -2), \ldots \}$$
Verify for yourself that the absolute value relation is an equivalence relation because it is reflexive, symmetric, and transitive. An interesting property of equivalence relations is that the partition a set into a set of equivalence classes where every element in a particular equivalence class is equivalent with respect to that particular equivalence relation. For example, the partitioning induced on the integers by the absolute value relation is shown below, where each equivalence class is represented as a set nested inside the set of all such classes, which represents the partition:
$$\{ \{0\},\ \{-1, 1\},\ \{-2, 2\}, \ldots \}$$
Another type of equivalence relation of interest two us is a modular congruence relation. We say that x is congruent to y modulo z, or in mathematical notation:
$$y \equiv x \mod z$$
This means that the remainder of x after division by z is the same as the remainder of y after division by z, which is sometimes represented by the notation:
$$x \% z = y \% z$$
A really simple example of this is the distinction between odd and even numbers. Odd and even numbers are the two congruence classes modulo 2; all even numbers have the same remainder (0) when divided by 2, and all odd numbers have the same remainder (1) when divided by 2.
Modular congruence relation are more complex and harder to represent in notation than the absolute value notation, so I will simply describe the modular congruence relation modulo 2 by noting that every even number is related to every other even number and every odd number is related to every other odd number, but no even number is related to any odd number, or vice versa.
Arithmetic Invariance
Invariance is a special property of equivalence relations that describes whether or not the equivalence of any two objects or elements is preserved after identical operations are performed on these "equivalent" elements. For example, the "right invariance" of equivalence relations on strings of characters is particularly useful in discussions about the regular languages. In this context, we're going to deal with a much simpler type of invariance: arithmetic invariance.
An equivalence relation is invariant with respect to a particular operation if and only if, for any two elements in the same equivalence class as each other, both of these elements remain in the same equivalence class as each other after application of the operation in question with the same arguments (if any). Note that the elements do not have to end in the same equivalence class that they started in; they just need to continue being equivalent to each other.
For example, the absolute value relation is invariant to multiplication by integers. The numbers 2 and -2 are equivalent with respect to absolute value, as are the numbers 6 and -6, which are the numbers produced by multiplying the first pair of numbers by 3.
Another way of depicting this is to say that for any function f on the domain S, and for any two elements x and z in S, the equivalence relation is invariant to f if:
$$x \equiv z \Rightarrow f(x) = f(z)$$
Now suppose S is the set of integers and f(x) = 3 * x. Then:
$$-2 \equiv 2 \Rightarrow f(-2) \equiv f(2)$$ $$-2 \equiv 2 \Rightarrow -2 \cdot 3 \equiv 2 \cdot 3$$ $$-2 \equiv 2 \Rightarrow -6 \equiv 6$$
However, the absolute value relation is NOT addition-invariant. Although -2 and 2 are equivalent, 5 and 1 do not have the same absolute value, so addition by 3 does not preserve the equivalence of the elements (the number 3 was chosen completely arbitrarily for sake of example in both cases).
$$-2 \equiv 2 \not \Rightarrow 5 \equiv 1$$
Because the absolute value relation is not invariant to addition, it is not arithmetic invariant. Arithmetic invariance requires that an equivalence relation is invariant to all the basic arithmetic operations.
You may have learned the rules at some point that any two even numbers add up to an even number, any two odd numbers add up to an even number, any even number plus any odd number equals an even number, any even number times any even number is even, any even number times any odd number is even, and any odd number times any odd number produces an odd number. The validity of these rules shows that the modular equivalence relation modulo 2 is invariant to both addition and multiplication. In general, modular congruence relations are fully arithmetic invariant.
Binary Numbers
If you look back to the ASCII table (http://www.asciitable.com/) that we referenced in part 1 of this post, you will notice that in addition to columns containing the decimal integers and the symbols, there are columns for hexadecimal and octal representations of integers and HTML. The reason hexadecimal and octal codes are useful is because they translate easily into binary numbers, which much more directly represent the way that computers store information.
Every conceivable kind of information that a computer stores or manipulates is represented in bits, which correspond to the voltage in some part of some circuit being either "high" or "low" according to some pre-defined thresholds with respect to some consistent reference value. The highness or lowness of voltages is a 2-state system that is very naturally represented by 0's and 1's, the only two digits used to represent numbers in a binary numeral system. This is a vast enough topic that it makes no sense for me to cover it in detail in my blog; see Wikipedia for details (https://en.wikipedia.org/wiki/Binary_number). One characteristic of interest, though, is that with positive numbers in binary notation, addition with pencil and paper works the same way that it does for decimal numbers, where you start from the one's place and carry overflow to the next lowest place.
The Sign & Magnitude Convention
Because computer's can't directly store arbitrary symbols or concepts such as a negative sign, the most straightforward way to represent negative numbers is to use a single bit (which can be 1 or 0) to represent the sign of a number (+ or -), since both a bit and a sign can have two states. The simplest way to do this is the sign and magnitude convention for storing negative numbers, where the first bit represents the sign, and all subsequent bits represent magnitude.
Consider the set of 3-bit binary numbers, ranging from 000 to 111. If we consider the leading 0 to represent + and the leading 1 to represent -, and the remaining bits to represent magnitude, then 001 = 1, 101 = -1, and 110 = -2. But how did we choose which negative numbers to assign to which bit strings? We chose the negative numbers with the same absolute value as the positive numbers with the same bit string (disregarding the sign bit). Remember, though, that the absolute value relation is NOT arithmetic invariant! Indded, if we perform arithmetic by pencil and paper as we do with decimal numbers, 001 + 101 = 101, which means 1 + -1 = -2. This doesn't make any sense. To make matters worse, not only is arithmetic with the sign & magnitude convention not intuitive on paper, it also requires more complex circuitry for the same reasons. This is one of the major reasons that the sign & magnitude convention is almost never used in modern computer systems.
Ones' Complement
In ones' complement, the first bit still indicates sign, but the trailing bits indicate magnitude only for positive numbers. For negative numbers, where the first bit is 1, the magnitude of the number is determined by flipping the trailing bits. For example, 101 has a magnitude of flip(01) = 10 = 2. Therefore, 101 = -2. Similarly, 110 has a magnitude of 01 = 1. Thus, even though 001 + 101 = 110, this means that -2 + 1 = -1 in ones' complement, which makes sense.
Why does this addition work so naturally in ones' complement? It's because ones' complement secretly relies on a modular congruence relation. Every negative number in ones' complement and the positive number that is represented by the same trailing bit string are in the same congruence class modulo x, where x equals (2 raised to the number of trailing bits) minus 1. With three bits, this magic number is 3. Notice that 1 % 3 = 1 = -2 % 3.
The main reason ones' complement is not the standard for representing negative numbers is that it allows for a representation of negative zero (111). This is unfortunate because checking if a value is equal to zero is an extremely common operation in computer programming, and in ones' complement systems this operation is slightly inefficient because one has to perform two checks instead of one, since there are two binary strings that represent 0: 000 and 111 (in our imaginary 3-bit system).
Two's Complement
Two's complement is extremely similar to ones' complement. The difference is that obtaining the magnitude of a negative number can be done by flipping the bits and then adding one, instead of just flipping the bits. This modification is done to ensure that even the most positive negative number (111) is equal to -1 instead of 0, ensuring that there is only 1 representation of 0. As a result of this, it is actually possible to store more negative numbers than positive numbers.
Two's complement also secretly relies on a modular congruence relation, the relation modulo (2 raised to the number of bits). In our 3 bit system, there are 2 trailing bits, so negative numbers and positive numbers represented by the same bit string are equivalent modulo 4. For example, 111 = -1, and 011 = 3; -1 % 4 = 3.
Knowing the underlying modular congruence relation can be useful in some fringe cases. The trick of flipping the bits and adding one doesn't work in every case. For example, if you are working with non-standard information formats, such as 24-bit integers, you may run into problems. I once had to work with a device that transmitted information stored in 24-bit integers at regular intervals. I was reading this information into a computer using a USB cable.
Unfortunately, the programming environment I was using on the computer required standard sized integers. Therefore, I had to convert the 24-bit integers into 32-bit integers. To my chagrin, all the integers were being interpreted as positive values, even though the data was actually signed voltage information. As a result, negative numbers were being interpreted as humongous positive numbers that were way off of the scale of the graph I was trying to display.
I tried casting the data explicitly to a signed integer, but that didn't work, because by left-padding the 24-bit integers with a byte of zeros to turn them into 32-bit integers, I had made all integers look positive to the computer! Whether I cast them as signed or unsigned, they represented the same positive value because of the leading zero. Next, I tried flipping the bits and adding 1, but that also flipped the padding zeros in the leading byte into 1s while turning the last 24 bytes into a small positive number, resulting in a humongous negative number instead of the small positive number storing the magnitude of the negative number, which was what I was trying to get at.
Finally, I ended up subtracting the incoming data by 2 raised to 24, which gave me exactly the values that I needed, because the interpreter was smart enough to realize that the result should be unsigned. This worked because adding or subtracting by a particular number produces a result which has the same remainder when divided by that number. For example, -1 % 4 = 3, and -1 + 4 = 3; 7 % 4 = 3, and 7 - 4 = 3. Do you see the pattern?
Decimal Complement
Another advantage of understanding how two's complement works from a set theoretical perspective is that we can extend the concept to arbitrary number systems, such as a hypothetical decimal system in which the functional units of our computer were somehow able to store 10 distinct states. In this case, we have 10 symbols, ranging in value from 0 to 9. Consider a 2-digit decimal string. There are 100 possible values we could store, ranging from 00 to 99.
If we want to store negative numbers, we could arbitrarily decide that any number greater than or equal to 50 will actually represent a negative number. That is, if the first digit is 5,6,7,8, or 9, this represents negative sign; if the first bit is 0,1,2,3, or 4, this represents positive sign. But which positive number will, for example, 55 represent? By analogy with 2's complement, we can just subtract from 100. 100 - 55 = 45, so 55 represents -45. Another way we can think about this is by "flipping" the digits across some imaginary threshold between 4 and 5 and then adding one. Thus 55 flipped becomes 44, and 44 + 1 = 45, so 55 = -45.
Notice that in this system, because there are 10 digits, the leading digit is able to simultaneously code for sign and magnitude! Isn't that cool? Such is the power of set theory and modular arithmetic.
Originally written on June 15, 2013 (ported from http://sandpapertiger.blogspot.com)