HOW TO BUILD A ROLLER COASTER
WITH ROCKET SCIENCE!
PART 3 OF 3
In the previous installment of this multi-part blog post, we saw a lot of theoretical math with some fairly complicated notation. Although there were pictures and explanations to help make the math as intuitive as possible, there were so many steps involved that it is difficult to come away feeling comfortable with the powerful, abstract equations and identities that we just derived. Therefore, it is worthwhile to reassure ourselves that the math actually makes sense. In order to do this, we can solve a very simple toy problem that we already know the answer to: in a Euclidean geometry, what is the shortest distance between two points? The answer, of course, is a straight line: as illustrated in the picture below,1 travel along a straight line makes the distance traveled equivalent to the displacement between two points, whereas other paths add unnecessary travel distance.
Since we noted earlier that distance is the integral of arc length, we can use this problem to test the validity of the calculus of variations. In part 1, we showed:
$$ds=\sqrt {1+y'^2}dx$$
$$\int_a^b \sqrt {1+y'^2}dx$$
$$\frac {\partial{F}} {\partial{q}} - \frac {\mathrm{d}} {\mathrm{d}x} \frac {\partial{F}} {\partial{q'}}$$
This equation describes an optimal solution q(x). In our work in part 1, we described a path using a depth variable y(x). To make our notation consistent, let us assume that y(x) = q(x), so y(x) now describes the depth profile of the shortest path. Then, we can restate the Euler-Lagrange equation in our context as:
$$\frac {\partial{F}} {\partial{y}} - \frac {\mathrm{d}} {\mathrm{d}x} \frac {\partial{F}} {\partial{y'}}$$
In this case, although the integrand does not depend on x, it is actually easier to solve the Euler-Lagrange equation directly than it is to apply the Beltrami identity. Therefore, let us proceed directly:
$$F = \sqrt {1+y'^2}$$ $$\frac {\partial{F}} {\partial{x}} = 0 \Rightarrow \frac {\mathrm{d}} {\mathrm{d}x} \frac {\partial{F}} {\partial{y'}} = 0$$
$$\frac {\mathrm{d}} {\mathrm{d}x} \left(\frac {1} {2} \left( 1 + y'^2 \right) \left( 2y' \right) \right) = 0$$
$$\frac {\mathrm{d}} {\mathrm{d}x} \left(\frac {y'} { \sqrt {1 + y'^2 }} \right) = 0$$
$$\mathrm{d} \left(\frac {y'} { \sqrt {1 + y'^2 }} \right) = 0 \mathrm{d}x$$
$$\frac {y'} { \sqrt {1 + y'^2 }} = C$$
$$y' = C \left( \sqrt {1 + y'^2} \right)$$
$$y'^2 \left(1 - C^2 \right) = C^2$$
And then we can rearrange this expression to show that:
$$y'^2 = \frac {C^2} { \left(1 - C^2 \right) }$$
$$y' = \pm \sqrt { \frac {C^2} { \left(1 - C^2 \right) } } $$
By squaring both sides earlier, we created a false solution, so only one of the two roots (positive or negative) is the correct slope. The sign of the slope depends on whether the starting point A is above or below the endpoint B. The exact value of the slope is, however, totally besides the point; we have no idea what the constant C is. All that matters is that we have expressed the slope of the curve, y', completely in terms of constants (1 and some unknown constant C), so the slope itself must be constant, and the optimal path must be a straight line. In terms of calculus, since our expression for y' consists solely of constants, y' does not depend on x:
$$ \frac { \mathrm{d}y' } { \mathrm{d}x } = y'' = 0$$
Integrate both sides, and call the constant m: $$y'=m$$
Integrate both sides again, and call the constant b this time: $$y = mx + b$$
Thus our optimal curve is described by the classic slope-intercept form equation for a line in the Cartesian plane. By solving the Euler-Lagrange equation, we demonstrated that the shortest path between two points is a straight line. We already know this is true from basic principles of geometry, so we have verified that the calculus of variations produces a sensible answer to the question we asked. Now that we understand how the solution process works in practice for a simple problem, we can comfortably use the methods derived in the previous post to solve more difficult problems. Let's proceed to the step we've all been waiting for: the solution to the brachistochrone problem!
The Solution
Unlike in the toy problem above, where y(x) described the depth problem of the shortest path, we are now looking for the fastest path from A to B. Therefore, we have to incorporate the results from part 1 that we derived using physics. Recall our integral for travel time in the brachistochrone problem:
$$t = \int_a^b \sqrt { \frac { 1 + y'^2 } { 2gy } }$$
The integrand here is more complex, so it pays to apply the Beltrami identity:
$$F - q' \frac { \partial{F} } { \partial{q'} } = C$$
Again, to make our notation consistent, let's rephrase this to describe the path in terms of the depth y:
$$F - y' \frac { \partial{F} } { \partial{y'} } = C$$
The function of interest is the integrand:
$$F = \int_a^b \sqrt { \frac { 1 + y'^2 } { 2gy } }$$
We can apply the quotient rule and chain rule to differentiate F:
$$\frac { \partial{F} } { \partial{y'} } = \frac { \sqrt { 2gy} \frac {1} {2} \left( 1 + y'^2 \right)^{-\frac {1} {2 } } \left(2y' \right) } {2gy }$$
$$\frac { \partial{F} } { \partial{y'} } = \frac { y'} { 2gy} \sqrt { \frac { 2gy} { 1+y'^2} }$$
Rearrange a little:
$$\frac { \partial{F} } { \partial{y'} } = \frac { y'} { \left( \sqrt { 2gy} \right)^2 } \sqrt { \frac { 2gy} { 1+y'^2} }$$
Now we can cancel some of the radicals containing gravity:
$$\frac { \partial{F} } { \partial{y'} } = \frac { y'^2} { \sqrt { 2gy} \sqrt { 1+y'^2} }$$
Thus:
$$F - y' \frac { \partial{F} } { \partial{y'} } = \frac { \sqrt { 1+y'^2} } { \sqrt { 2gy} } - \frac { y'^2} { \sqrt { 2gy} \sqrt { 1+y'^2} }$$
$$\frac { \sqrt { 1+y'^2} } { \sqrt { 2gy} } - \frac { y'^2} { \sqrt { 2gy} \sqrt { 1+y'^2} } = C$$
Factor out the radical containing gravity:
$$\frac { 1 } { \sqrt { 2gy} } \left( \sqrt { 1+y'^2} - \frac { y'^2} { \sqrt { 1+y'^2} } \right) = C$$
Manipulate the terms in parentheses to achieve a common denominator:
$$\frac { 1 } { \sqrt { 2gy} } \left( \sqrt { 1+y'^2} \frac { \sqrt { 1+y'^2}} { \sqrt { 1+y'^2}} - \frac { y'^2} { \sqrt { 1+y'^2} } \right) = C$$
$$\frac { 1 } { \sqrt { 2gy} } \left( \frac { 1+y'^2} { \sqrt { 1+y'^2}} - \frac { y'^2} { \sqrt { 1+y'^2} } \right) = C$$
$$\frac { 1 } { \sqrt { 2gy} } \left( \frac { 1+y'^2 - y'^2 } { \sqrt { 1+y'^2}} \right) = C$$
The y' terms in the numerator cancel:
$$\frac { 1 } { \sqrt { 2gy} \sqrt { 1+y'^2}} = C$$
Rearrange slightly:
$$\frac { 1 } { C \sqrt { 2gy} } = \sqrt { 1+y'^2}$$
Square both sides:
$$\frac { 1 } { 2gyC^2 } = 1+y'^2 $$
C is some arbitrary constant from the Beltrami identity, so the value of the constants is not relevant at this point. We are just trying to find some curve where the right side of the above equation is constant. Therefore, let us simplify the expression by by introducing a new constant to consolidate all the old constants:
$$k = \frac {1} {2gC^2}$$ $$ \frac {k} {y} = 1 + y'^2$$
Rearrange again: $$y'^2 = \frac {k} {y} - 1$$ $$\frac {\mathrm{d} x} {\mathrm{d} y} = \sqrt{ \frac{k} {y} - 1}$$
Combine terms in the radical:
$$\frac {\mathrm{d} x} {\mathrm{d} y} = \sqrt{ \frac{k} {y} - \frac {y} {y}}$$ $$\frac {\mathrm{d} x} {\mathrm{d} y} = \sqrt{ \frac{k - y} {y}}$$
Use separation of variables to solve for x:
$$\frac {\mathrm{d} y} {\sqrt { \frac {k-y} {y} } } = \mathrm{d} x$$ $$\int \left( \frac{ 1- k^2y} {k^2 y} \right)^{ - \frac {1} {2} } \mathrm{d} y = \int \mathrm{d} x$$ $$\int \sqrt { \frac {y} {k-y} } \mathrm{d} y = \int \mathrm{d} x$$ $$x = \int \sqrt { \frac {y} {k-y} } \mathrm{d} y$$
Now we need to perform a complicated trigonometric substitution:
$$y = \frac {k} {2} \left[1 - \mathrm{cos} \left(\theta \right) \right]$$
Apply a trigonometric identity to simplify the integration step:
$$\mathrm{cos} \left(2 \theta \right) = 1 - 2 \mathrm{sin}^2 \left(\theta \right)$$ $$\mathrm{cos} \left( \theta \right) = 1 - 2 \mathrm{sin}^2 \left( \frac {\theta} {2} \right)$$ $$ y = \frac {k} {2} \left[1 - \left(1 - 2 \mathrm{sin}^2 \left(\frac {\theta} {2} \right) \right) \right]$$ $$ y = k \mathrm{sin}^2 \left(\frac {\theta} {2} \right)$$ $$ \mathrm{d} y = k \mathrm{sin} \left(\frac {\theta} {2} \right) \mathrm{cos} \left(\frac {\theta} {2} \right) \mathrm{d} \theta$$
Substituting these into our integral expression for x: $$x = \int \sqrt { \frac k {\mathrm{sin}^2 \left(\frac {\theta} {2} \right)} {k - k \mathrm{sin}^2 \left(\frac {\theta} {2} \right)} } k \mathrm{sin} \left(\frac {\theta} {2} \right) \mathrm{cos} \left(\frac {\theta} {2} \right) \mathrm{d} \theta$$
Cancel the constant k from inside the radical:
$$x = \int \sqrt { \frac {\mathrm{sin}^2 \left(\frac {\theta} {2} \right)} {1 - \mathrm{sin}^2 \left(\frac {\theta} {2} \right)} } k \mathrm{sin} \left(\frac {\theta} {2} \right) \mathrm{cos} \left(\frac {\theta} {2} \right) \mathrm{d} \theta$$
Apply another trigonometric identity:
$$ \mathrm{sin}^2 \left(\frac {\theta} {2} \right) + \mathrm{cos}^2 \left(\frac {\theta} {2} \right) = 1$$
$$ \mathrm{cos}^2 \left(\frac {\theta} {2} \right) = 1 - \mathrm{sin}^2 \left(\frac {\theta} {2} \right) $$
$$x = \int \sqrt { \frac {\mathrm{sin}^2 \left(\frac {\theta} {2} \right)} {\mathrm{cos}^2 \left(\frac {\theta} {2} \right)} } k \mathrm{sin} \left(\frac {\theta} {2} \right) \mathrm{cos} \left(\frac {\theta} {2} \right) \mathrm{d} \theta$$
$$x = \int \frac {\mathrm{sin} \left(\frac {\theta} {2} \right)} {\mathrm{cos} \left(\frac {\theta} {2} \right)} k \mathrm{sin} \left(\frac {\theta} {2} \right) \mathrm{cos} \left(\frac {\theta} {2} \right) \mathrm{d} \theta$$
Cancel the cosines and consolidate:
$$x = \int k \mathrm{sin}^2 \left(\frac {\theta} {2} \right) \mathrm{d} \theta$$
Reapply a familiar trigonometric identity:
$$ \mathrm{sin}^2 \left(\frac {\theta} {2} \right) + \mathrm{cos}^2 \left(\frac {\theta} {2} \right) = 1$$
$$ \mathrm{cos}^2 \left(\frac {\theta} {2} \right) = 1 - \mathrm{sin}^2 \left(\frac {\theta} {2} \right) $$
$$x = \int k \left[ 1 - \mathrm{cos}^2 \left(\frac {\theta} {2} \right) \right] \mathrm{d} \theta$$
Apply another trigonometric identity:
$$\mathrm{cos} \left(2 \theta \right) = 2 \mathrm{cos}^2 \left(\theta \right) - 1$$ $$\mathrm{cos} \left(\theta \right) = 2 \mathrm{cos}^2 \left( \frac {\theta} {2} \right) - 1$$ $$\mathrm{cos} \left(\theta \right) + 1 = 2 \mathrm{cos}^2 \left( \frac {\theta} {2} \right)$$ $$\mathrm{cos}^2 \left( \frac {\theta} {2} \right) = \frac {\mathrm{cos} \left(\theta \right) + 1} {2} $$
Substituting this into our integrand:
$$x - \int k \left[1 - \frac {\mathrm{cos} \left(\theta \right) + 1} {2} \right] \mathrm{d} \theta$$
$$x - \int k \left[1 - \frac {\mathrm{cos} \left(\theta \right)} {2} - \frac {1} {2} \right] \mathrm{d} \theta$$
$$x - \int k \left[\frac {1} {2} - \frac {\mathrm{cos} \left(\theta \right)} {2} \right] \mathrm{d} \theta$$
$$x - \frac {k} {2} \int \left[1 - \mathrm{cos} \left(\theta \right) \right] \mathrm{d} \theta$$
$$x - \frac {k} {2} \left[\theta - \mathrm{sin} \left(\theta \right) \right]$$
Thus we have produced a set of parametric equations:
$$x - \frac {k} {2} \left[\theta - \mathrm{sin} \left(\theta \right) \right]$$
$$y - \frac {k} {2} \left[1 - \mathrm{cos} \left(\theta \right) \right]$$
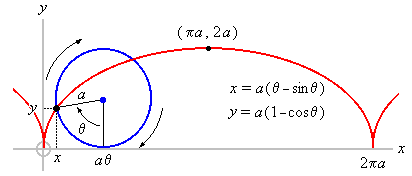
We have solved the brachistochrone problem! Thanks to Caltech2 for notes on some of the less intuitive substitution steps. The above expressions for x and y are a complete description of the optimal path that the rollercoaster must take to get from A to B as quickly as possible using the acceleration of gravity. The only detail we ignored were the integration constants that would be determined in the context of a problem with specific numbers by the exact x and y coordinates of points A and B. The shape of the curve is the same, though; it's merely the offset that changes with these constants. Curiously, the shape described by these equations is equivalent to an upside-down rotation of a section of the path traced out by a point on the edge of a wheel as it rolls along a flat surface, also called a cycloid3 See the picture below from BCIT:4
A great description of the origin of the brachistochrone problem as a challenge posed by Jakob Bernoulli, and its relation to the rivalries between great mathematicians of the era, can be found at the University of ST. Andrews Website.5
Acknowledgements
It turns out that optimization theory is useful for far more than just rocket science. In particular, it is heavily used in medical image analysis, especially of MRI images, in biomedical research. Special thanks to Professor Paul Yushkevich at the University of Pennsylvania for first introducing me to the field of optimization theory in this context.
- http://en.wikipedia.org/wiki/Distance
- http://www.hep.caltech.edu/~fcp/math/variationalCalculus/variationalCalculus.pdf
- http://en.wikipedia.org/wiki/Cycloid
- http://commons.bcit.ca/math/entertainment/coaster/index.html
- http://www-history.mcs.st-and.ac.uk/HistTopics/Brachistochrone.html
Originally written in January 2013; ported from http://sandpapertiger.blogspot.com