HOW TO BUILD A ROLLER COASTER

WITH ROCKET SCIENCE!

PART 2 OF 3

photo-1433094657682-205abd5f883b.jpg.png

GRADIENT DESCENT

If you know calculus, you should be familiar with using differentiation to find extrema (maxima or minima of a function). For example, suppose we live in a valley surrounded by infinitely large mountains, and the shape of the valley is perfectly described by representing the elevation above sea level, e, as a function of position, p, according to the following equation:

$$e=(p-2)^2+3$$

At the lowest point in the valley, any change in position must increase the elevation. Since the valley slopes up both to the right and to the left, the tangent to the curve of the valley floor is horizontal and the slope is equal to zero. Therefore, in order to find the specific p-coordinate, p*, of the lowest point in the valley, we take the derivative of e with respect to p and set it equal to zero.

$$\frac{\mathrm{d}e}{\mathrm{d}p}=2(p-2)$$
$$\frac{\mathrm{d}e}{\mathrm{d}p}=2p-4$$
$$\frac{\mathrm{d}e}{\mathrm{d}p} \biggr\rvert _{p=p^*}=0$$
$$2(p^*-4)=0$$
$$2p^*=4$$
$$p^*=2$$
$$e(p^*)=e(2)=(2-2)^2+3$$
$$e(p^*)=3=e_{min}$$

In this example, we were easily able to extremize a function (elevation) by taking its derivative with respect to the variable of interest (position) and setting that derivative equal to zero. Any solutions to the resulting equation are extrema, or points where the elevation function has local minima or maxima. In this problem it was obvious that the solution was a minimum, but if we weren't sure, we would have to check that the second derivative was positive at that point to make sure the solution was a minimum. Also, in this case, there was only one solution to the extremization equation. If there were multiple extrema, there would be multiple solutions. If several of these were minima, we would then have to check our work by calculating the elevation (e) value at each position (p) with a local minimum elevation in order to choose the position with the lowest elevation. That would be the global minimum, and the true global solution (except in cases with a bounded domain, when the endpoints might be global extrema without necessarily solving the extremization equation).

Let us return to the brachistochrone problem. In this problem, it is not immediately apparent how we can apply the principles of calculus to solve the problem. The function we are trying to minimize is a complex integral that represents the amount of time taken to traverse a path. The variable that we can modify is the shape of the path. If time and path were variables on perpendicular axes like position and elevation, we could simply solve the following equation:

$$\frac{\mathrm{d}time}{\mathrm{d}path}=0$$

THE EULER-LAGRANGE EQUATION

Unfortunately, time and path are not orthogonal. Therefore, we have to do some theoretical juggling to extend the method of finding extrema by differentiation into this context. The key trick is to think about how to represent the "path" mathematically. When faced with this problem, several famous mathematicians, notably Euler, made significant advances leading to a new field of mathematics called the calculus of variations. From the calculus of variations, the Euler-Lagrange equation provides us with the tools we need to find an optimal curve with the minimum value of the line integral of some function. I will attempt to explain the logic behind the Euler-Lagrange equation below. I am going to follow the notation used by the Wikipedia page on the Euler-Lagrange equation.¹ However, I have added notes and reordered steps where I felt it was necessary to make the explanation here more intuitive, even if less rigorous, than the explanation on Wikipedia.

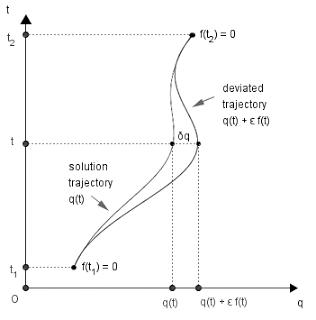
Any smooth, single-valued path between A and B can be represented by some function y = g(x) that describes the y-value of each point along the path (the height of the roller-coaster track at that point) in terms of its horizontal distance (x) from A towards B. Such a function contains all of the information we need to describe the shape of the path. We can think of the optimal path as a special function y = q(x). Now for any path that is different from this ideal path q(x), we can treat the non-ideal path g(x) as a distorted version of q(x). Specifically, we can represent g(x) mathematically as the sum of q(x) and some function η(x) which represents the deviation of g(x) from the ideal shape of q(x).

$$g(x)=q(x)+\eta(x)$$
However, in order to apply the concept of differentiation to find extrema, we need to be able to vary the shape of the path under consideration in some manner. Therefore, instead of representing g(x) as a simple sum, we represent it as a weighted sum and weight the distortion function η(x) by some coefficient of distortion ε.

$$g(x)=q(x)+ \epsilon \eta(x)$$

The picture below, from a lecture notes website,² nicely illustrates this concept. The picture uses slightly different notation: it calls the distortion function f(t) instead of η(x). Disregard the labels if you find them confusing.

Before we proceed, we need to place some restrictions on the distortion function η(x). Since the only functions g(x) that we are considering are the ones that provide paths from A to B, the function g(x) begins and ends at the same endpoints as q(x) - points A and B. Let us call their x-coordinates a and b respectively. Then:

$$g(a)=q(a)$$

But from our weighted sum representation of g:

$$g(a)=q(a)+ \epsilon \eta(a)$$

Combining these equations:

$$\epsilon \eta(a) = 0$$

This is true regardless of the function g in question, so g is not necessarily equal to q, meaning that ε is not necessarily zero. Thus:

$$\eta(a)=0$$

By symmetry:

$$\eta(b)=0$$

Within those limits, any smooth distortion function η(x) can be used as needed to produce some smooth path g(x) under consideration. Now let us consider a path-dependent variable of interest J which has an optimal value on the ideal path q(x). Using the trick above, we can represent variations in path by changes in the distortion coefficient ε. When ε = 0, g(x) = q(x). For any nonzero distortion function η(x), changing ε from zero to any positive or negative value will produce some change in g(x) that makes it different from q(x). Since q(x) is the optimal path, this will produce a suboptimal value of the variable J that we are trying to extremize. We may need to represent different paths g(x) using different distortion functions η(x), but for any such path and any such distortion it still holds true that there is an extreme value of J when ε = 0, since we have defined q(x) to be the optimal path. If the value of J on q(x) is a local minimum, then J increases when we change ε in either direction; if it is a maximum, then J decreases when we change ε in either direction. In either case, it is true that:

$$\frac{\mathrm{d}J}{\mathrm{d}\epsilon} \biggr\rvert _{\epsilon=0}=0$$

This result holds true in general for any path-dependent variable J. In practice, however, the variable of interest, J, is often the line integral along the path in question of another function F. This is true in the brachistochrone problem as well as in many other applications. Therefore, let us suppose we have some function F whose value along the path depends on the coordinates of the path (x and g(x)) and its slope (g'(x)):

$$F = F(x,g(x),g'(x))$$

Or, for simplicity's sake:

$$F=F(x,g,g')$$

Let J then be the integral of F as x increases from a to b (we are preserving our convention from earlier that a and b are the x-values of the path's endpoints).

$$J=\int_a^b F(x,g,g') dx$$

Based on our earlier work, we know that the derivative of J with respect to ε must equal zero when ε is zero. But it is not immediately obvious how to differentiate J with respect to ε, since J is the integral of another function F. We need to somehow evaluate the derivative of that integral:

$$\frac{\mathrm{d}J}{\mathrm{d}\epsilon} = \frac{\mathrm{d}}{\mathrm{d}\epsilon} \int_a^b F(x,g,g') dx$$

Apply the Leibniz integral rule³ to interchange integral and differential operators:

$$\frac{\mathrm{d}J}{\mathrm{d}\epsilon} = \int_{x_1}^{x_2} \frac{\mathrm{d} F(x,g,g') }{\mathrm{d}\epsilon} dx$$

Rewrite the total derivative⁴ in terms of partial derivatives using the chain rule:

$$\frac{\mathrm{d}F}{\mathrm{d}\epsilon} = \frac{\partial F}{\partial x} \frac{\mathrm{d} x}{\mathrm{d} \epsilon } + \frac{\partial F}{\partial g} \frac{\mathrm{d} g}{\mathrm{d} \epsilon } + \frac{\partial F}{\partial g'} \frac{\mathrm{d} g'}{\mathrm{d} \epsilon } $$

As we change ε, the path g(x) changes because the contribution of the distortion η(x) changes as we alter its weight. Since g(x) is changing, g'(x) may also change. However, x itself does not change; we are still integrating over the same stretch of x-coordinates between a and b. Therefore:

$$\frac{\mathrm{d}x}{\mathrm{d}\epsilon} = 0$$
$$\frac{\mathrm{d}F}{\mathrm{d}\epsilon} = \frac{\partial F}{\partial g} \frac{\mathrm{d} g}{\mathrm{d} \epsilon } + \frac{\partial F}{\partial g'} \frac{\mathrm{d} g'}{\mathrm{d} \epsilon } $$

Substituting in:

$$g(x) = q(x) + \epsilon \eta(x)$$

$$\frac{\mathrm{d}F}{\mathrm{d}\epsilon} = \frac{\partial F}{\partial g} \eta(x) + \frac{\partial F}{\partial g'} \eta'(x)$$

$$\frac{\mathrm{d}J}{\mathrm{d}\epsilon} = \int_a^b \frac{\partial F}{\partial g} \eta(x) + \frac{\partial F}{\partial g'} \eta'(x) \mathrm{d}x$$

$$\frac{\mathrm{d}J}{\mathrm{d}\epsilon} \biggr\rvert _{\epsilon=0} = \int_a^b \frac{\partial F}{\partial g} \eta(x) + \frac{\partial F}{\partial g'} \eta'(x) \mathrm{d}x = 0$$

$$\int_a^b \frac{\partial F}{\partial g} \eta(x) dx + \int_a^b \frac{\partial F}{\partial g'} \eta'(x)dx =0$$

We can now use integration by parts⁵ to simplify this expression. From the product rule, we know that for any two differentiable functions u and v, the following holds true about their product uv:

$$\mathrm{d}(uv)= u\mathrm{d}v + v \mathrm{d}u$$

From this we can derive a convenient formula for integration by parts:

$$\int_a^b \mathrm{d}(uv)= \int_a^b u\mathrm{d}v + \int_a^b v \mathrm{d}u$$

$$uv \biggr\rvert _a^b = \int_a^b u\mathrm{d}v + \int_a^b v \mathrm{d}u$$

$$uv \biggr\rvert _a^b - \int_a^b v \mathrm{d}u = \int_a^b u\mathrm{d}v $$

$$\int_a^b u\mathrm{d}v = uv \biggr\rvert _a^b - \int_a^b v \mathrm{d}u$$

We can then apply integration by parts to evaluate the second integral term in our expression on F:

$$\int_a^b \frac{\partial F}{\partial g'} \eta'(x) \mathrm{d}x = ?$$

$$u=\frac{\partial F}{\partial g'}$$

$$\mathrm{d}v = \eta'(x) \mathrm{d}x$$

$$v = \int \mathrm{d}v = \int \eta'(x) \mathrm{d}x = \eta(x)$$

$$\mathrm{d}u = \frac{\mathrm{d}u}{\mathrm{d}x} \mathrm{d}x = \frac{\mathrm{d}}{\mathrm{d}x} \frac{\partial F}{\partial g'} \mathrm{d}x$$

$$\int_a^b \frac{\partial F}{\partial g'} \eta'(x) \mathrm{d}x = \frac{\partial F}{\partial g'} \eta(x) \biggr\rvert_a^b - \int_a^b \frac{\mathrm{d}}{\mathrm{d}x} \frac{\partial F}{\partial g'} \eta(x) \mathrm{d}x$$

Now we can substitute this result into the original two-term expression:

$$\int_a^b \frac{\partial F}{\partial g} \eta(x) \mathrm{d}x + \int_a^b \frac{\partial F}{\partial g'} \eta'(x) \mathrm{d}x = 0$$

$$\int_a^b \frac{\partial F}{\partial g} \eta(x) \mathrm{d}x + \frac{\partial F}{\partial g'} \eta(x) \biggr\rvert_a^b - \int_a^b \frac{\mathrm{d}}{\mathrm{d}x} \frac{\partial F}{\partial g'} \eta(x) \mathrm{d}x = 0$$

$$\int_a^b \frac{\partial F}{\partial g} \eta(x) \mathrm{d}x - \int_a^b \frac{\mathrm{d}}{\mathrm{d}x} \frac{\partial F}{\partial g'} \eta(x) \mathrm{d}x + \frac{\partial F}{\partial g'} \eta(x) \biggr\rvert_a^b = 0$$

$$\int_a^b \frac{\partial F}{\partial g} \eta(x) - \frac{\mathrm{d}}{\mathrm{d}x} \frac{\partial F}{\partial g'} \eta(x) \mathrm{d}x + \frac{\partial F}{\partial g'} \eta(x) \biggr\rvert_a^b = 0$$

$$\int_a^b \left( \frac{\partial F}{\partial g} - \frac{\mathrm{d}}{\mathrm{d}x} \frac{\partial F}{\partial g'} \right) \eta(x) \mathrm{d}x + \frac{\partial F}{\partial g'} \eta(x) \biggr\rvert_a^b = 0$$

We can apply the constraint that the distortion is zero at the endpoints:

$$\eta(a) = \eta(b) = 0$$

$$\frac{\partial F}{\partial g'} \eta(x) \biggr\rvert_a^b = \frac{\partial F}{\partial g'} (\eta(b)-\eta(a)) = \frac{\partial F}{\partial g'} (0-0) = \frac{\partial F}{\partial g'} \times 0 = 0$$

Substituting this result into our previous expression:

$$\int_a^b \left( \frac{\partial F}{\partial g} - \frac{\mathrm{d}}{\mathrm{d}x} \frac{\partial F}{\partial g'} \right) \eta(x) \mathrm{d}x = 0$$

Thus:

$$\frac{\mathrm{d}J}{\mathrm{d}\epsilon} \biggr\rvert _{\epsilon=0} = \int_a^b \left( \frac{\partial F}{\partial g} - \frac{\mathrm{d}}{\mathrm{d}x} \frac{\partial F}{\partial g'} \right) \eta(x) \mathrm{d}x = 0$$

The key insight that we need to apply now is that the equation above holds true for all functions g(x) under the condition that ε = 0. Therefore, it is true regardless of the nature of the distortion function η(x); the equation is valid for all values of η(x) that meet the constraints of the problem. Under the condition that ε = 0, however, g(x) becomes equal to q(x), so we can rewrite the equation as

$$\int_a^b \left( \frac{\partial F}{\partial q} - \frac{\mathrm{d}}{\mathrm{d}x} \frac{\partial F}{\partial q'} \right) \eta(x) \mathrm{d}x = 0$$

Then, because this is true for any distortion function η(x), we can apply the fundamental lemma of the calculus of variations⁶ to produce a differential equation involving F, q, and x that can be solved to find the optimal curve y = q(x):

Euler-Lagrange Equation¹

$$\frac{\partial F}{\partial q} - \frac{\mathrm{d}}{\mathrm{d}x} \frac{\partial F}{\partial q'} = 0$$

The last step is not intuitive, so it is worth justifying in rough terms the logic of the fundamental lemma of the calculus of variations. Let us suppose we know of a function u(x) and we know that u(x) has the property that:

$$\int_a^b u(x) v(x) dx=0$$

Furthermore, let us suppose that we know that the above expression is true for every possible function v(x) under the constraints that v(x) is a smooth function and v(a) = v(b) = 0. This means that we can pick an arbitrary v(x) that we like that is smooth and zero-valued at these endpoints, and we still know that the integral specified will evaluate to zero. Now let us take advantage of this and pick a function v(x) that is positive everywhere that u(x) is positive (except at x = a and x = b, where v(x) = 0 by constraint). Let as also construct our function v(x) so that it is negative everywhere u(x) is negative (again, except at x = a and x = b, where v(x) = 0 by constraint). As a consequence of this, v(x) will cross between positive and negative signs in the same places as u(x), so v(x) = 0 ONLY where u(x) = 0 and where x = a or x = b.

If we construct v(x) in this manner, then the multiple of the two functions, u(x)v(x), must be positive or zero everywhere, since two positive values multiply to produce a positive number, and two negative values multiply to produce a positive number. Since integration measures the area under a curve, the integral of this function from a to b can only be zero if the curve itself is zero everywhere between a and b, since there are no regions where function is negative, which could cancel out other positive regions. Therefore, since we know that the integral evaluates to zero, the multiple _u(x)v(x) = 0 _everywhere between a and b. This isn't the case because we set v(x) = 0; rather, we let v(x) have the same sign as u(x) everywhere except the endpoints, so v(x) = 0 between a and b only where u(x) = 0. So if the multiple u(x)v(x) is zero everywhere between a and b, it must be because u(x) = 0 everywhere between a and b. Thus, u(x) = 0. This is the gist of the fundamental lemma of the calculus of variations, although a formal proof is much more arcane.

In the derivation of the Euler-Lagrange equation, we knew that the entire integral expression evaluates to zero for any distortion function η(x). That means we can pick an arbitrary function η(x) that is zero at the endpoints of the path and smooth with respect to differentiation, and it must still hold true that the integral of η(x) multiplied by the differential expression evaluates to zero. By analogy to the above argument, we can conclude that the Euler-Lagrange equation must hold true; the differential expression is equal to zero. This produces a differential equation that can be solved for the optimal path q(x).

Remember, though, that we assumed in our derivation of the Euler-Lagrange equation that F was a function of the following form:

$$F = F(x,g,g')$$

This is a very general class of functions, so the result, in the form of the Euler-Lagrange equation, is applicable to a wide variety of interesting problems. Currently, however, we are interested in the following integral in the brachistochrone problem:

$$t = \int_a^b \! \frac{\sqrt{1+y'^2} \mathrm{d}x}{\sqrt{2gy}}$$
$$t = \int_a^b \! \sqrt{\frac{1+y'^2}{2gy}} \, \mathrm{d}x$$

If we represent the optimal curve as some function y = q(x), and paths from A to B in general as functions y = g(x), then t is analogous to the variable of interest J in the derivation of the Euler-Lagrange equation above. Whereas J is an integral of F(x, g(x), g'(x)), the travel time t is an integral of F(g(x), g'(x)). The integrand in the brachistochrone problem does not explicitly depend on x:

$$\frac{\partial F}{\partial x} = 0$$

Or, in the specific context of the brachistochrone problem,

$$\frac{\partial \sqrt{\frac{1+y'^2}{2gy}} } {\partial x}= 0$$

THE BELTRAMI IDENTITY

In special cases such as these, it is not necessary to solve the full Euler-Lagrange equation, which is overly general and more difficult to solve. Instead, we can manipulate the Euler-Lagrange equation to express it in terms of the partial derivative of F with respect to x. Then, we can apply the Beltrami identity⁷ to simplify the Euler-Lagrange equation for those cases where F does not vary with x.

$$\frac{\partial F}{\partial q} - \frac{\mathrm{d}}{\mathrm{d}x} \frac{\partial F}{\partial q'} = 0$$

Multiply both sides by q':

$$\frac{\partial F}{\partial q} q' - \frac{\mathrm{d}}{\mathrm{d}x} \frac{\partial F}{\partial q'} q' = 0$$

As before, we can represent a total derivative in terms of partial derivatives using the chain rule:

$$\frac{\mathrm{d}F}{\mathrm{d}x} = \frac{\partial F}{\partial q} \frac{\mathrm{d} q}{\mathrm{d} x } + \frac{\partial F}{\partial \frac{\mathrm{d} q}{\mathrm{d} x } } \frac{\mathrm{d}^2 q}{\mathrm{d} x^2 } + \frac{\partial F}{\partial x} \frac{\mathrm{d} x}{\mathrm{d} x } $$

We can simplify this by using ' to denote differentiation with respect to x, and noting that dx/dx = 1:

$$\frac{\mathrm{d}F}{\mathrm{d}x} = \frac{\partial F}{\partial q} q' + \frac{\partial F}{\partial q' } q'' + \frac{\partial F}{\partial x} $$

This can be rearranged to show that:

$$ q' \frac{\partial F}{\partial q} = \frac{\mathrm{d}F}{\mathrm{d}x} - \frac{\partial F}{\partial q' } q'' - \frac{\partial F}{\partial x} $$

We can substitute this into the modified Euler-Lagrange equation, which produces:

$$\frac{\mathrm{d}F}{\mathrm{d}x} - \frac{\partial F}{\partial q' } q'' - \frac{\partial F}{\partial x} - q' \frac{\mathrm{d}}{\mathrm{d} x} \frac{\partial F}{\partial q'} = 0$$

Again, from the chain rule, we know that:

$$\frac{\mathrm{d}} {\mathrm{d}x} \left( \frac{\partial F} {\partial q'} q' \right) = \frac{\partial F} {\partial q'} \frac{\partial q'} {\partial x} + q' \frac{\mathrm{d}} {\mathrm{d}x} \frac{\partial F} {\partial q'}$$

$$\frac{\mathrm{d}} {\mathrm{d}x} \left( \frac{\partial F} {\partial q'} q' \right) = \frac{\partial F} {\partial q} q'' + q' \frac{\mathrm{d}} {\mathrm{d}x} \frac{\partial F} {\partial q'}$$

$$\frac{\mathrm{d}} {\mathrm{d}x} \left( \frac{\partial F} {\partial q'} q' \right) - \frac{\partial F} {\partial q} q'' = q' \frac{\mathrm{d}} {\mathrm{d}x} \frac{\partial F} {\partial q'}$$

$$q' \frac{\mathrm{d}} {\mathrm{d}x} \frac{\partial F} {\partial q'} = \frac{\mathrm{d}} {\mathrm{d}x} \left( \frac{\partial F} {\partial q'} q' \right) - \frac{\partial F} {\partial q} q''$$

We can again substitute this back into our further modified equation:

$$\frac{\mathrm{d}F}{\mathrm{d}x} - \frac{\partial F}{\partial q' } q'' - \frac{\partial F}{\partial x} - \left[\frac{\mathrm{d}} {\mathrm{d}x} \left( \frac{\partial F} {\partial q'} q' \right) - \frac{\partial F} {\partial q} q''\right] = 0$$

We can now cancel the q'' terms (the second one has double negative signs):

$$\frac{\mathrm{d}F}{\mathrm{d}x} - \frac{\partial F}{\partial x} - \frac{\mathrm{d}} {\mathrm{d}x} \left( \frac{\partial F} {\partial q'} q' \right) = 0$$

We can rearrange this to show:

$$\frac{\mathrm{d}}{\mathrm{d}x} \left(F - \frac{\partial F}{\partial q'} q' \right) - \frac{\partial F} {\partial x} = 0$$

However, we are considering cases where:

$$ \frac{\partial F} {\partial x} = 0$$

Therefore, we know that:

$$\frac{\mathrm{d}}{\mathrm{d}x} \left(F - \frac{\partial F}{\partial q'} q' \right) = 0$$

Integrating both sides, we conclude:

Beltrami Identity

$$F - \frac{\partial F}{\partial q'} q' = C$$

for some constant C. Now we have all the mathematical tools that we need to solve the brachistochrone problem. Next time, we will see how to apply these tools to find the exact solution.