Pokémon are really interesting creatures. They gain experience, and then use this experience to evolve. Different precursor Pokémon evolve into different evolved forms. We can represent these relationships with an evolution diagram that connects precursor Pokémon to their evolutions with arrows. I like pictures, but I'm bad at art, so all pictures in this blog post are from the Bulbapedia.¹

(Per Bulbapedia policy, the Bulbapedia content is used with attribution, and the modified Bulbapedia images here are reusable under the same license).

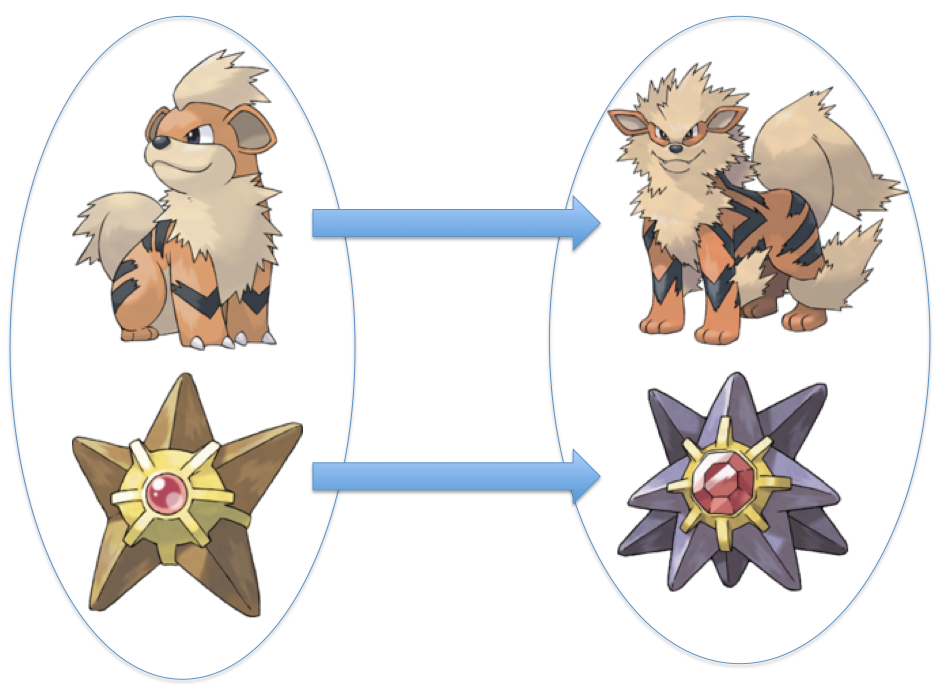
The diagram above shows that Growlithe evolves into Arcanine, and that Staryu involves Starmie. Diagrams like this can help us believe that everything is right in the world; everyone has their proper place in the order of things. We could make our diagram bigger to involve more Pokémon. Ideally, if all of the Pokémon that can evolve were on the left of our diagram, and all the Pokémon that result from evolutions were on the right of our diagram, we might be able to make a diagram with all the Pokémon in the universe! In that case, every time we caught a Pokémon, we could look it up in our diagram. Precursor Pokémon would show up on the left side, so we could figure out exactly what they evolve into, and evolved Pokémon would up on the right side of our diagram, we could figure out exactly what they evolved from. Wouldn't this be exciting? Before we try to make a complete diagram, though, let's try a few more smaller ones as practice. For simplicity, let's only consider Generation 1 Pokémon so we don't get overwhelmed.

Oh no! Something has gone terribly wrong. Our beautiful plan of figuring out exactly what each precursor Pokémon evolves into is ruined. When my Eevee was discussing its career plans with me, I showed it this diagram, and it got really confused. In fact, it hurt itself in its confusion! This made me very upset. Let's try again.

Oops! It seems like we are in trouble again. Nothing evolves into Aerodactyl. When my Aerodactyl saw this diagram, it realized that if it ever had children, they wouldn't be cute little precursor Pokémon like the little Pichu babies the neighbor's Raichu just had, but instead would be just as bony and ugly as itself. Then it threw a tantrum and destroyed half my kitchen. Now I have to eat take-out Weepinbell sprouts with synthetic Gloom sauce from Gary's Garden, a low-quality "health food" joint run by a former Pokémon trainer who has fallen on bad times. My stomach is sad.

It turns out that I should never have dreamed about a universal Pokémon evolution diagram with every precursor Pokémon pointing to a single evolved form. Let me explain why, so you never have to suffer through what I've suffered through.

Let me use a few math words to help explain what is happening. The word "set" means a collection of things, like a bag that contains certain things and only those things. We call the things contained in a set its elements. We like to describe a set by providing a list of the elements contained in the set enclosed in curly braces. For example, the empty set contains no elements, so nothing appears between the braces:

$$\{\}$$

We use the word "tuple" to mean an ordered list of elements. Like a set, a tuple contains certain elements and only those elements, but it lists them in a specific order. For example, these two sets are equivalent:

$$\{peanut\ butter, jelly\}$$

$$\{jelly, peanut\ butter\}$$

Since each set is like a bag containing the number one and the number two, and order doesn't matter. When I'm making PB&J, I don't really care which slice has what, as long as it's all in the sandwich. However, this isn't true for tuples. We write tuples by listing the elements in order between parentheses. In this representation, these two tuples are different:

$$(cook,eat)$$

$$(eat,cook)$$

I usually like to cook my food before I eat it, because after I've eaten the food is a bit harder to get at.

Now I've talked about sets and tuples. We also use the word "relation" to mean a set where each element is a tuple. A binary relation is a special kind of relation where each of the tuples has exactly two elements; these tuples are ordered pairs.

In the context of evolution in Pokémon, the binary relation we are interested in is pairs of Pokémon where the first Pokémon involves into the second. We represent ordered pairs as a list of elements between parentheses. So, the first diagram I made contained a pair we could write like this:

$$(Growlithe, Arcanine)$$

The full first diagram represented a relation we could write like this:

$$\{(Growlithe, Arcanine), (Staryu, Starmie)\}$$

The pictures are much nicer. Writing these out can get tedious. However, it helps for some purposes, so let's also describe the second diagram in writing:

$$\{(Eevee, Flareon), (Eevee, Vaporeon), (Eevee, Jolteon)\}$$

The problem that we noticed in the diagram is now visible in a different fashion: the name Eevee is repeated multiple times in the first elements of different pairs. We call a relation that maps every input to a single output a "function." In a functional evolution relation, a precursor Pokémon could map to two evolutions only if those evolutions are also the exact same Pokémon. The same precursor Pokémon could not map to any two different evolutions in a functional relation. Because Eevee is repeated multiple times in the first elements of different pairs, this relation is not a function.

Maybe we can fix this by reversing the order of the diagram? Then, it would look like this:

This relation is a function. The problem now is that Eevee is repeated multiple times in the second element of different pairs. We call a relation injective if two elements map to the same precursor only if they are also the same as each other. With Pokémon, two evolved forms could map to the same precursor only if they are also the same Pokémon, so no two different evolved forms could map to the same precursor. However, that does happen in this diagram, so this function is not injective.

Finally, we can represent the third diagram (with Aerodactyl) as a relation in set notation:

$${}$$

Although there is a Pokémon in the third diagram, there are no pairs of Pokémon, so the relation is equivalent to the empty set. That's not the reason that the diagram is a problem, though. If we added Aerodactyl to the first diagram, the new diagram would look like this:

The set theory notation for this relation is still:

$$\{(Growlithe, Arcanine), (Staryu, Starmie)\}$$

Now we see that the real problem with this relation is that it doesn't say anything at all about Aerodactyl, even though Aerodactyl is in the diagram. In math, when we describe diagrams like the ones above, we call the set of elements shown on the left side of the diagram the domain, and we call the set of elements shoown on the right side of the diagram the range or co-domain. We call a function surjective with respect to a particular domain and range if every element in the range is contained in the map because it is paired with some element in the domain. In a surjective relation, every evolved form of a Pokémon displayed in the diagram would be contained in the map because it would be paired with some precursor. Unfortunately, this relation is not surjective as long as we include Aerodactyl as part of the range by displaying it in the diagram.

Now that we know about functionality, injectivity and surjectivity, we can see that the first diagram was a function that was both injective and surjective. These kinds of relations are called bijective functions, or bijections. It turns out that if a relation is a bijection, that means that the set of elements in the domain is exactly the same size as the set of elementsi n the range. In theory, this is true even for infinitely large sets: if we show that there exists a bijection between two infinitely large sets, then these sets are infinitely large with the same order of infinity. This means that there are some countably infinite sets, meaning that there exists a bijection between those sets and the set of natural, counting numbers, and some nondenumerably (uncountably) infinite sets, for which no such bijection exists. Mind-boggling, right? Anyway, we can't make a full Pokémon evolution diagram that has the properties we wanted at the beginning, because the evolution relation is not bijective on the set of all Pokémon, not even on just Generation 1 Pokémon. So don't even bother. You'll just end up eating take-out Weepinbell sprouts with synthetic Gloom sauce from Gary's Garden.

Originally written in January 2013; ported from http://sandpapertiger.blogspot.com